게임업계에서 길찾기 알고리즘에 많이 사용된다는 JPS알고리즘을 공부했다. JPS알고리즘은 A* 알고리즘과 유사하지만 대부분의 경우 A* 알고리즘보다 성능이 좋다고 한다.
우선 JPS의 핵심은 Jump Point를 찾는 것인데 그 Jump Point만 열린 목록에 넣고 A*에서 하듯이 비용을 검사한다. 당연히 A*처럼 가능한 모든 경로에 있는 노드들을 열린 목록에 넣고 검사하는 것이 아니라 비용이 더 적다.
Jump Point를 찾는 방법은 2가지가 있는데 첫번째 방법은 Jumping Straight경우를 살펴보는 것이다.

Jumping Straight
Figure(a)가 Jumping Straight Case이다. p(x)는 x의 부모이다. p(x) 기준으로 상하좌우 중에서 오른쪽으로만 갈 수 있으니 오른쪽으로 쭉 간다. 이때 쭉 가면서 진행 방향의 왼쪽(또는 오른쪽)이 막혀있고 왼쪽 대각선 방향(혹은 오른쪽 대각선 방향) 이 갈 수 있는 곳이라면 그곳은 새로운 Jump Point가 될 수 있다. Figure(a)가 정확히 이 예시이므로 y가 새로운 Jumping Point가 될 수 있다. 참고로 Figure(a)의 양쪽 대각선 화살표 방향의 타일도 Figure(b)의 Jumping Diagonally Case에 의해 새로운 Jumping Point가 될 수 있다.
Jumping Straight case에서 중요한 점은 상하좌우 방향으로 쭉 나아가다가 타일맵의 끝에 도달하거나 막힌다면 그 루트는 새로운 Jump Point가 될 수 없다. 반드시 진행 방향의 왼쪽(또는 오른쪽)이 막혀있고 왼쪽 대각선 방향(혹은 오른쪽 대각선 방향) 이 갈 수 있는 곳이어야한다.
Jumping Diagonally
Figure(b)가 Jumping Diagonally Case이다. 대각선으로 한칸씩 가면서, 대각선으로 한 칸 이동해간 타일에서 다시 Recursive하게 Jumping Straight Case를 검사해보는것이다. (b)의 경우 대각선으로 한칸씩 이동해서 검사해도 전부 벽에 막히거나 타일맵 끝에 도달해버려서 결국 y까지에 도달한 후, 상하좌우 중에 가보지 않은 곳이거나, 막히지 않은 곳이 오른쪽 방향이므로 y->z로 이동하는데, z에 도달해보니 Jumping Straight Case처럼 진행 방향의 오른쪽이 막혀 있고, 오른쪽 대각선이 갈 수 있으므로 z는 새로운 Jumping Point가 되는 것이다.
이 두가지 규칙을 예시에 적용해보자

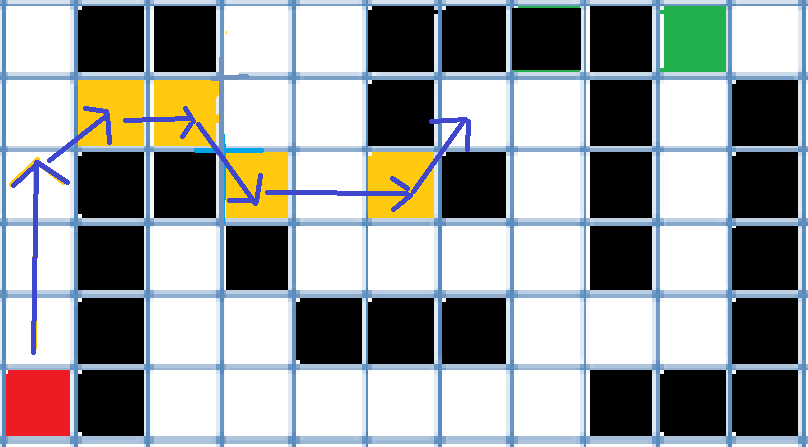
빨간색 타일이 시작점이고, 초록색 타일이 도착점이다.


시작점에서 위로 쭉 가다가 오른쪽이 막히고, 오른쪽 대각선이 갈 수 있는 곳이므로 노란 타일은 새로운 Jump Point가 될 수 있다. 노란색 타일에서 갈 수 있는 곳은 오른쪽이므로 오른쪽으로 한칸씩 가면서 Jumping Straight Case인지를 검사하면 바로 오른쪽 타일이 새로운 Jump Point인 것을 알 수 있다.


마지막 Jump Point에서 이렇게 두 경우를 생각해보자. 위 대각선의 경우 가봤자 다시 Jumping Straight Case를 따져보면 만족하는 경우가 없다. 오른쪽으로 가려는 경우는 아래가 막혀있고 오른쪽 대각선 방향이 갈 수 있는 타일이므로 오른쪽 그림에서 볼 수 있듯이 새로운 Jump Point를 찾았다.
마지막 Jump Point에서 또 다시 상하좌우를 쭉 가서 보면 아래 그림처럼 Jumping Diagonally Case에 해당하는 Jump Point를 찾을 수 있다.
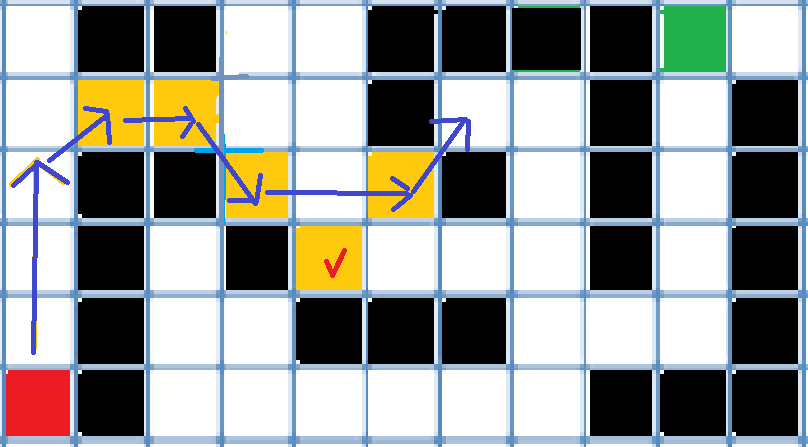
물론 오른쪽 그림에서 빨간색 체크된 부분도 새로운 Jump Point가 될 수 있다.
이렇게 두가지 규칙에 기반해서 새로운 Jump Point를 찾는다면 결론적으로 아래와 같은 그림이 될 것이다.
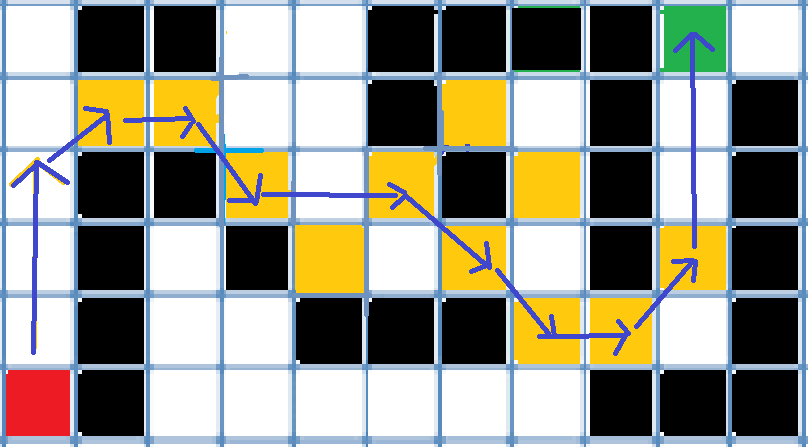
대략적인 흐름은 이런 알고리즘 같은데 추가적으로 관련된 논문이나 영어로 소개된 글을 더 읽고 공부해봐야겠다.
개인적인 공부 목적으로 작성한 글이고 계속 공부하면서 수정중에 있으므로, 틀린 내용이 있을 수 있습니다.
Reference
https://harablog.wordpress.com/2011/09/07/jump-point-search/
Jump Point Search
This is the final article in my three-part look at symmetry reduction algorithms for speeding up pathfinding on uniform-cost grid maps. Recapping the story so far: Part one introduces the notion of…
harablog.wordpress.com
https://zerowidth.com/2013/a-visual-explanation-of-jump-point-search.html
zerowidth positive lookahead | A Visual Explanation of Jump Point Search
A Visual Explanation of Jump Point Search Please note: this post contains SVG diagrams rendered with javascript. Please view it in a browser to see all the content. There are several related algorithms for finding the shortest path on a uniform-cost 2D gri
zerowidth.com
'공부 > Algorithm' 카테고리의 다른 글
| Dijkstra algorithm(다익스트라 알고리즘) 구현 (0) | 2021.08.11 |
|---|---|
| 병합 정렬(Merge sort) (0) | 2021.08.10 |
| DFS(Depth First Search) & BFS(Breadth First Search) (0) | 2021.08.10 |
| 마스터 정리(Master Method), Big-Oh, Theta, Omega Notation (0) | 2021.08.07 |
| 힙 정렬 (Heap Sort) 구현 (0) | 2021.08.07 |