// Heapsort.h
#pragma once
#include <cmath>
#include <assert.h>
template <typename T>
class CHeapsort
{
public:
CHeapsort()
{
m_Capacity = 10;
m_Size = 0;
m_Data = new T[m_Capacity];
}
~CHeapsort()
{
delete[] m_Data;
}
private:
T* m_Data;
int m_Size;
int m_Capacity;
private:
void MaxHeapify(int Index)
{
int Left = Index * 2;
int Right = Index * 2 + 1;
// Left와 Right중 큰 element의 인덱스
int LargeIndex = Index;
// MinHeap으로 바꾸고 싶다면 여기 등호 반대로
if (Left <= m_Size && m_Data[Left] > m_Data[LargeIndex])
{
LargeIndex = Left;
}
// MinHeap으로 바꾸고 싶다면 여기 등호 반대로
if (Right <= m_Size && m_Data[Right] > m_Data[LargeIndex])
{
LargeIndex = Right;
}
if (LargeIndex != Index)
{
T temp = m_Data[LargeIndex];
m_Data[LargeIndex] = m_Data[Index];
m_Data[Index] = temp;
MaxHeapify(LargeIndex);
}
}
void BuildMaxHeap()
{
for (int i = floor(m_Size / 2); i > 0; --i)
{
MaxHeapify(i);
}
}
public:
// heap에 데이터를 넣기만 하는 함수(정렬은 Heapsort 호출해야함)
// 인덱스 1부터 넣는다
void PushData(const T& Data)
{
if (m_Capacity == m_Size + 1)
{
m_Capacity *= 2;
T* temp = new T[m_Capacity];
memcpy(temp, m_Data, sizeof(T) * m_Capacity);
delete[] m_Data;
m_Data = temp;
}
m_Data[m_Size+1] = Data;
++m_Size;
}
void Heapsort()
{
BuildMaxHeap();
for (int i = m_Size; i > 1; --i)
{
T temp = m_Data[1];
m_Data[1] = m_Data[i];
m_Data[i] = temp;
--m_Size;
MaxHeapify(1);
}
}
int GetSize() const
{
return m_Size;
}
int GetCapacity() const
{
return m_Capacity;
}
T GetTop() const
{
return m_Data[1];
}
T* GetData() const
{
return m_Data;
}
T GetData(int Index) const
{
return m_Data[Index];
}
bool empty() const
{
return m_Size == 0;
}
};
// main.cpp
#include <iostream>
#include <time.h>
#include "Heapsort.h"
#include <crtdbg.h>
int main()
{
_CrtSetDbgFlag(_CRTDBG_ALLOC_MEM_DF | _CRTDBG_LEAK_CHECK_DF);
CHeapsort<int> heap;
srand((unsigned int)time(0));
rand();
for (int i = 0; i < 20; ++i)
{
int random = rand();
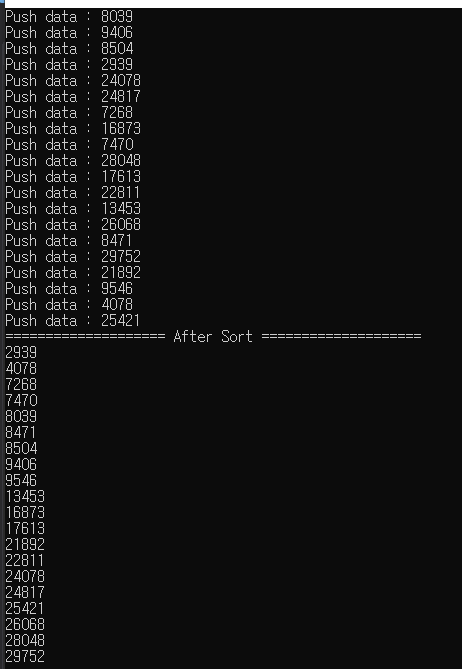
std::cout << "Push data : " << random << std::endl;
heap.PushData(random);
}
int Size = heap.GetSize();
heap.Heapsort();
std::cout << "==================== After Sort ====================" << std::endl;
for (int i = 1; i <= Size; ++i)
{
std::cout << heap.GetData(i) << std::endl;
}
return 0;
}
MaxHeapify를 점화식으로 표현하면
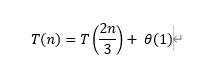
이렇게 표현할 수 있다(n은 노드의 개수). 왜냐하면 MaxHeapify에서는 각 서브트리로 MaxHeapify를 재귀 호출 하는데, 서브트리의 최대 노드 수가 2n/3 이기 때문이다. 2n/3의 노드 개수에 대해 MaxHeapify를 재귀 호출하므로 저런 점화식으로 표현 가능한 것이다. 위의 식을 마스터 정리로 풀면 T(n) = O(log n) 이 나온다(마스터 정리 글은 여기 정리 https://welikecse.tistory.com/manage/newpost/?type=post&returnURL=%2Fmanage%2Fposts)
TISTORY
나를 표현하는 블로그를 만들어보세요.
www.tistory.com
MaxHeapify가 O(log n)이고 BuildMaxHeap의 시간 복잡도를 구해보자. 트리에서 높이 h에 존재할 수 있는 최대 노드수는 다음과 같이 표현할 수 있다.

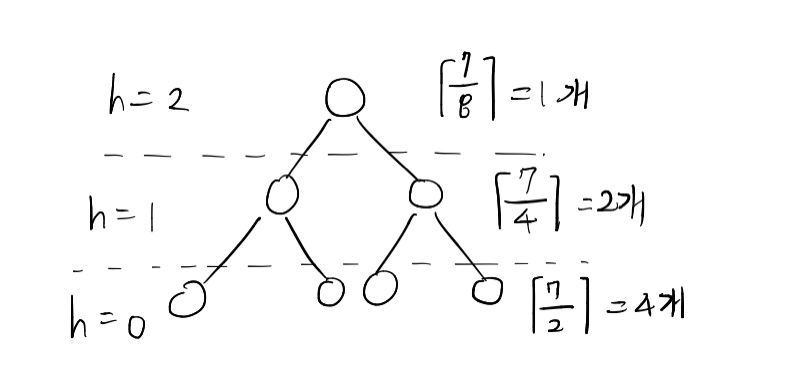
높이가 h일때 최대 저만큼의 노드가 있을 수 있다는 의미이므로 높이 h = 0부터 트리의 높이까지 BuildMaxHeap의 시간 복잡도는 다음과 같이 표현될 수 있다.

그런데 무한 등비 급수 공식에 의해 아래와 같이 정리될 수 있다.

마지막으로 heapsort는 BuildMaxHeap을 한번 호출( Time complexity : O(n) ) + n-1번 MaxHeapify호출(Time complexity : O(nlogn) )
따라서 Heapsort의 시간 복잡도는 O(n) + O(nlogn) = O(nlogn)이 된다.
heapsort는 최악, 평균의 경우 모두 O(nlogn)을 보장한다
'공부 > Algorithm' 카테고리의 다른 글
| JPS(Jump Point Search) Algorithm (0) | 2022.02.17 |
|---|---|
| Dijkstra algorithm(다익스트라 알고리즘) 구현 (0) | 2021.08.11 |
| 병합 정렬(Merge sort) (0) | 2021.08.10 |
| DFS(Depth First Search) & BFS(Breadth First Search) (0) | 2021.08.10 |
| 마스터 정리(Master Method), Big-Oh, Theta, Omega Notation (0) | 2021.08.07 |